Aufgabenbeispiele von Winkel
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Innenwinkel im Dreieck
Beispiel:
Gegeben ist das Dreieck ABC mit A, B und C. Berechne den Innenwinkel des Dreiecks im Punkt A.
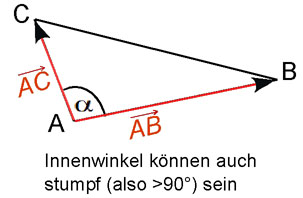 Wir berechnen den Winkel zwischen
den Vektoren =
und =
Wir berechnen den Winkel zwischen
den Vektoren =
und =
also
Winkel zwischen zwei Vektoren
Beispiel:
Berechne den Winkel zwischen den Vektoren
Wir bilden
(wie immer bei Winkeln) das Sklarprodukt der beiden Vektoren, also von
Der Betrag des normierten Skalarprodukts ist gleich dem cos des gesuchten Winkels zwischen den Ebenen.
 Wir berechnen den Winkel zwischen
den Vektoren
Wir berechnen den Winkel zwischen
den Vektoren
also
Winkel zwischen 2 Geraden
Beispiel:
Berechne den Winkel unter dem sich die Geraden
g:
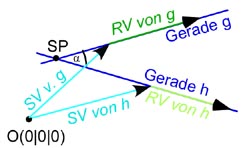 Wir bilden (wie immer bei Winkeln) das Sklarprodukt von den Richtungsvektoren der beiden Geraden, also von
Wir bilden (wie immer bei Winkeln) das Sklarprodukt von den Richtungsvektoren der beiden Geraden, also von Der Betrag des normierten Skalarprodukts ist gleich dem cos des gesuchten Winkels zwischen den sich schneidenden Geraden.
also Schnittwinkel
Winkel zwischen 2 Ebenen
Beispiel:
Berechne den Winkel zwischen den Ebenen
E:
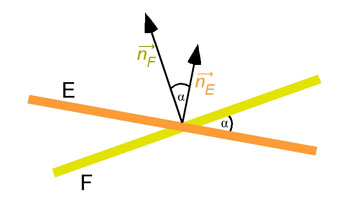 Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von
Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von
Der Betrag des normierten Skalarprodukts ist gleich dem cos des gesuchten Winkels zwischen den Ebenen (weil dieser ja gleich ist, wie der zwischen den Normalenvektoren).
also Schnittwinkel
Winkel zwischen Ebene und Gerade
Beispiel:
Berechne den Winkel zwischen der Ebene
E:
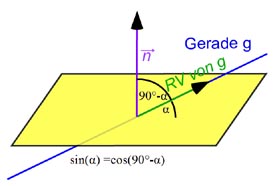 Wir bilden (wie immer bei Winkeln) das Sklarprodukt,
Wir bilden (wie immer bei Winkeln) das Sklarprodukt, diesesmal von Normalenvektor der Ebene
Da wir so ja eigentlich den Winkel zwischen Normalenvektor und Gerade berechnen würden, müssen wir das diesesmal = sin(α) setzen.
also Schnittwinkel
Innenwinkel im Dreieck
Beispiel:
Gegeben ist das Dreieck ABC mit A
 Wir berechnen den Winkel zwischen
den Vektoren
Wir berechnen den Winkel zwischen
den Vektoren
also
Winkel in der Pyramide
Beispiel:
Gegeben ist eine Pyramide mit einer quadratischen Grundfläche ABCD, die in der x1-x2-Ebene liegt und die Kantenlänge 5 besitzt.
Der Punkt D liegt im Ursprung (0|0|0). Die Spitze der Pyramide hat die Koordinaten S
a) Berechne den Innenwinkel α zwischen der Grundfläche ABCD und der Seitenfläche DAS
b) Berechne den Innenwinkel β zwischen den beiden Seitenflächen DAS und CDS
Beide Winkel können als Schnittwinkel zwischen zwei Ebenen berechnet werden. Dazu benötigen wir erstmal die drei Normalenvektoren:
- Die Grundfläche ABCD in der x1-x2-Ebene x3=0 hat natürlich den
Normalenvektor
( 0 0 1 ) - Der Normalenvektor der Ebene, in der das Dreieck DAS liegt, muss orthogonal zu
DS → ( 1 1 7 ) DA → ( 5 0 0 ) n1 → ( 0 7 -1 ) ( 0 7 -1 ) ( 1 1 7 ) ( 0 7 -1 ) ( 5 0 0 ) - Der Normalenvektor der Ebene, in der das Dreieck CDS liegt, muss orthogonal zu
DS → ( 1 1 7 ) DC → ( 0 5 0 ) n2 → ( 7 0 -1 ) ( 7 0 -1 ) ( 1 1 7 ) ( 7 0 -1 ) ( 0 5 0 )
Natürlich hätte man die Normalenvektoren auch mit dem Vektorprodukt berechnen können.
a)Berechnung des Innenwinkel α zwischen der Grundfläche ABCD und der Seitenfläche DAS:
Man erkent (auch mit der Skizze) leicht, dass dieser Winkel spitz (also kleiner als 90°) sein muss. Deswegen können wir diesen Innenwinkel einfach als den
(spitzen) Schnittwinkel zwischen den zwei Ebenen mit den Normalenvektoren
also
b)Berechnung des Innenwinkel β zwischen den beiden Seitenflächen DAS und CDS:
Hier ist es sehr viel schwieriger zu erkennen, ob der Winkel zwischen den beiden Seitenflächen spitz oder stumpf ist. Am besten kann man es entscheiden, wenn man sich das Dreieck ACD anschaut und dabei den Punkt D auf der Kante AD nach oben laufen lässt. Solange D noch in der Grundebene liegt ist der Winkel in D noch 90°. Wenn der Punkt aber dann die Kante DS hochläuft, wird der Abstand des laufenden Punkts zur Strecke AC kleiner und dadurch der Winkel in diesem laufenden Punkt größer und damit stumpf. Dies gilt auch dann, wenn der laufende D-Punkt in einer zu beiden Seitenflächen orthogonalen Ebene liegt, und somit der Winkel im Dreieck gleich ist wie der gesuchte zwischen den Seitenflächen.
Der Winkel β ist also stumpf. Deswegen berechnen wir erstmal den Winkel zwischen den Normalenvektoren der beiden Seitenflächen
also
Der gesuchte stumpfe Winkel ist somit β = 180° - 88.9 ≈ 91.1°
