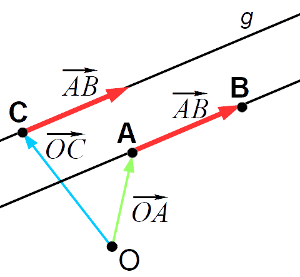Wir stellen zuerst mit dem Ortsvektor von A als Stützvektor und dem Verbindungvektors $\overrightarrow{\mathrm{AB}}$ als Richtungsvektor die Gerade durch A und B auf:

$\overrightarrow{\mathrm{AB}}$ = = $\left(\begin{array}{c}5\\ -2\\ 5\end{array}\right)$

Somit gilt für die Gerade durch A und B: $\overrightarrow{x}$ = $\overrightarrow{\mathrm{0A}}$ + t ⋅ $\overrightarrow{\mathrm{AB}}$, also :

$\overrightarrow{x}$ = $\left(\begin{array}{c}-4\\ -5\\ 1\end{array}\right)$ + t ⋅ $\left(\begin{array}{c}5\\ -2\\ 5\end{array}\right)$

Da die gesuchte Gerade ja parallel zur Geraden durch A und B sein soll, können wir für diese doch einfach den gleichen Richtungsvektor $\overrightarrow{\mathrm{AB}}$ = $\left(\begin{array}{c}5\\ -2\\ 5\end{array}\right)$ nehmen. Lediglich als Stützvektor ersetzen wir nun den Ortsvektor von A mit dem von C:

Somit gilt für die Gerade durch A und B: $\overrightarrow{x}$ = $\overrightarrow{\mathrm{0C}}$ + t ⋅ $\overrightarrow{\mathrm{AB}}$, also :

$\overrightarrow{x}$ = $\left(\begin{array}{c}4\\ 1\\ -5\end{array}\right)$ + t ⋅ $\left(\begin{array}{c}5\\ -2\\ 5\end{array}\right)$

Um zu überprüfen, ob P auf der Geraden g liegt, setzen wir diesen einfach in die Geradengleichung ein:

$\left(\begin{array}{c}2\\ -2\\ -2\end{array}\right)$ = $\left(\begin{array}{c}2\\ -1\\ -2\end{array}\right)+t\cdot \left(\begin{array}{c}-4\\ 8\\ -8\end{array}\right)$

2 = 2 -4t |-2
-2 = -1 +8t |+1
-2 = -2 -8t |+2

0 = -4t, also t = $0$
-1 = 8t, also t = $-\frac{1}{8}$
0 = -8t, also t = $0$

Da es kein t gibt, das in allen drei Gleichungen zu einer wahren Aussage führt, liegt der Punkt P also nicht auf der Geraden.

Wenn der Punkt P auf der Geraden liegen soll, kann man dessen Ortsvektor ja in die Geradengleichung ganz links für das $\overrightarrow{x}$ einsetzen:

$\left(\begin{array}{c}a\\ 5\\ 2\end{array}\right)$ = $\left(\begin{array}{c}11\\ 20\\ -13\end{array}\right)+t\cdot \left(\begin{array}{c}4\\ 5\\ -5\end{array}\right)$

Wir betrachten nun jede Zeile für sich und versuchen das t zu bestimmen, falls kein a in der Zeile vorkommt:

a = 11+4⋅t

5 = 20+5⋅t=> 5⋅t = -15 also t = -3

2 = -13-5⋅t=> -5⋅t = 15 also t = -3

Setzen wir nun diese t = -3 in die 1-te Zeile ein, so erhalten wir:
a = 11-12, also gilt: a = -1

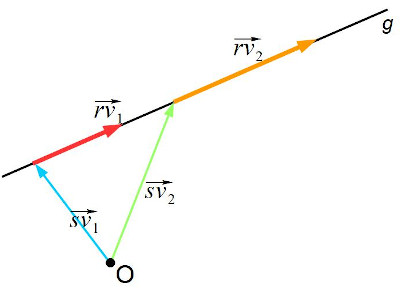Wir beginnen mit dem Richtungsvektor, der ja ein Vielfaches des Richtungsvektors der gegebenen Geraden $\left(\begin{array}{c}-1\\ 0\\ 1\end{array}\right)$ sein muss.

Es muss also gelten:

$\left(\begin{array}{c}-1\\ 0\\ 1\end{array}\right)$ = r ⋅ $\left(\begin{array}{c}-3\\ \mathrm{x2}\\ \mathrm{x3}\end{array}\right)$

Man sieht schnell, dass r = $\frac{1}{3}$ sein muss.

Somit muss auch 0 = $\frac{1}{3}$ ⋅ x2, also x2 = 0 sein .

Somit muss auch 1 = $\frac{1}{3}$ ⋅ x3, also x3 = 3 sein .

Der gesuchte Richtungsvektor ist also $\left(\begin{array}{c}-3\\ 0\\ 3\end{array}\right)$ und wir können g entweder als $\overrightarrow{x}=$ $\left(\begin{array}{c}1\\ -3\\ -3\end{array}\right)+t\cdot \left(\begin{array}{c}-1\\ 0\\ 1\end{array}\right)$ oder als $\overrightarrow{x}=$ $\left(\begin{array}{c}1\\ -3\\ -3\end{array}\right)+t\cdot \left(\begin{array}{c}-3\\ 0\\ 3\end{array}\right)$ schreiben.

Jetzt brauchen wir noch einen Punkt auf der Geraden mit -5 in der x3-Koordinate, den wir als Stützvektor benutzen können.

Um diesen zu bestimmen nehmen wir am besten die Geradendarstellung mit den kleineren Zahlen im Richtungsvektor. Wir suchen also s1 und s2 damit gilt:

$\left(\begin{array}{c}\mathrm{s1}\\ \mathrm{s2}\\ -5\end{array}\right)$ = $\left(\begin{array}{c}1\\ -3\\ -3\end{array}\right)+t\cdot \left(\begin{array}{c}-1\\ 0\\ 1\end{array}\right)$

Hier betrachten wir natürlich die 3. Zeile, in der steht:
-5 = -3 + t ⋅ 1 | +3
-2 = t ⋅ 1
-2 = t

Wenn wir also t=-2 in die Geradengleichung einsetzen erhalten wir als Ortsvektor eines Geradenpunkts $\left(\begin{array}{c}1\\ -3\\ -3\end{array}\right)-2\cdot \left(\begin{array}{c}-1\\ 0\\ 1\end{array}\right)$ = $\left(\begin{array}{c}3\\ -3\\ -5\end{array}\right)$.

Dieser hat an der x3-Koordinate die geforderte und kann als Stützvektor benutzt werden. Die gesuchte Geradengleichung ist damit:
$\overrightarrow{x}=$ $\left(\begin{array}{c}3\\ -3\\ -5\end{array}\right)+t\cdot \left(\begin{array}{c}-3\\ 0\\ 3\end{array}\right)$

Da die beiden Geraden windschief zueinander sind, darf der Richtungsvektor von h nicht gleich dem von g oder ein Vielfaches davon sein. Am geschicktesten ist es, wenn man als Richtungsvektor von h einen ganz einfachen Vektor nimmt, z.B.: $\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$.

Als Stützvektor von h könnten wir beispielweise den Stützvektor von g nehmen und ihn in der x₂-Koordinate um eins erhöhen, also $\left(\begin{array}{c}1\\ -2\\ 3\end{array}\right)$.

So können wir sicher sein, dass sich g und h keinen gemeinsamen Punkt haben können, weil ja alle Punkte auf der Geraden h nun -2 als x₂-Koordinate und 3 als x₃-Koordinate haben. Aber der einzige Punkt auf g, der 3 als x₃-Koordinate hat, muss ja -3 als x₂-Koordinate haben, weil ja dann der Parameter t in der Geraden g den Wert 0 annehmen muss. Somit kann es keinen Punkt P(x₁|-2|3) auf g geben und damit keinen gemeinsamen Punkt mit h (auf der alle Punkte die Form P(x₁|-2|3) haben.

Es ergibt sich also als eine möglich Gerade h: $\overrightarrow{x}=$ $\left(\begin{array}{c}1\\ -2\\ 3\end{array}\right)+t\cdot \left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$

Die beiden Richtungsvektoren $\left(\begin{array}{c}3\\ 1\\ -8\end{array}\right)$ und $\left(\begin{array}{c}6\\ 2\\ -16\end{array}\right)$ der Geraden sind linear abhängig (Vielfache voneinander). Wir müssen also prüfen, ob die Geraden parallel oder identisch sind.
Setzen wir daher den Stützvektor der zweiten Geraden $\left(\begin{array}{c}-14\\ -15\\ 12\end{array}\right)$ in die erste Gerade ein.

Es gibt kein t, welches diese Gleichung erfüllt. Der Stützvektor $\left(\begin{array}{c}4\\ -1\\ 2\end{array}\right)$ der ersten Geraden liegt also nicht auf der Geraden $\overrightarrow{x}=$ $\left(\begin{array}{c}-14\\ -15\\ 12\end{array}\right)+t\cdot \left(\begin{array}{c}6\\ 2\\ -16\end{array}\right)$.
Somit sind die beiden Geraden parallel.

Wenn die beiden Geraden echt parallel sein sollen, müssen die beiden Richtungsvektoren Vielfache voneinander sein, es muss also gelten:

r ⋅ $\left(\begin{array}{c}-5\\ -4\\ 4\end{array}\right)$ = $\left(\begin{array}{c}b\\ 8\\ -8\end{array}\right)$

Man erkennt leicht, dass wegen der 2. und 3. Zeile ein Gleichheit nur für r = $-2$ möglich sein kann. Wenn wir also b = $-2$ ⋅ -5 = 10 setzen so gilt $-2$ ⋅ $\left(\begin{array}{c}-5\\ -4\\ 4\end{array}\right)$ = $\left(\begin{array}{c}b\\ 8\\ -8\end{array}\right)$.

Somit muss also b = 10 sein.

Mit diesem b wissen wir nun, dass die Richtungsvektoren der beiden Geraden Vielfache voneinander sind. Somit kann die gegenseitige Lage der beiden Geraden nur noch echt parallel oder identisch sein.

Damit nun die beiden Geraden aber auch wirklich echt parallel und nicht identisch sind, müssen wir sicherstellen, dass g und h keinen gemeinsamen Punkt haben.
Der einfachste Fall zum Rechnen wäre, wenn zufällig bereits der Aufpunkt von h $\left(5|\mathrm{a}|-11\right)$ auf g liegen würde. Deswegen untersuchen wir mal, ob es ein a gibt, so dass der Aufpunkt von h $\left(5|\mathrm{a}|-11\right)$ auf g liegt.

Wir setzen also $\left(\begin{array}{c}5\\ a\\ -11\end{array}\right)$ = $\left(\begin{array}{c}-5\\ 2\\ -3\end{array}\right)+t\cdot \left(\begin{array}{c}-5\\ -4\\ 4\end{array}\right)$,

Dazu betrachten wir die 3. Zeile :

und die 1. Zeile:

In beiden Fällen muss t also $-2$ sein. Setzen wir nun dieses t = $-2$ auch noch in die 2. Zeile ein, so erhalten wir:

a = 2 + $\left(-2\right)$ ⋅ ( - 4 ) = 10.

Für a = 10 würde also der Aufpunkt von h (5|10|-11) auf der Geraden g liegen, denn

$\left(\begin{array}{c}5\\ 10\\ -11\end{array}\right)$ = $\left(\begin{array}{c}-5\\ 2\\ -3\end{array}\right)+\mathrm{<math\; xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo>-</mo><mn>2</mn></mrow></math>}\cdot \left(\begin{array}{c}-5\\ -4\\ 4\end{array}\right)$

Das soll ja aber gerade nicht sein. Deswegen müssen wir einen anderen Wert für a wählen, z.B. a = 11, damit der Aufpunkt von h (5|11|-11) nicht auf g liegt. (So erhalten wir einen anderen Wert für t in der 2. Zeile.)

Da die Richtungsvektoren Vielfache voneinander sind, könnnen die Geraden ja nur noch parallel oder identisch sein. Da nun aber der Aufpunkt von h (5|11|-11) nicht auf g liegt, können sie nicht mehr identisch sein.

Zuerst berechnet man den Vektor $\overrightarrow{\mathrm{AB}}$ = = $\left(\begin{array}{c}0\\ 8\\ -6\end{array}\right)$.
Damit können wir gleich mal den Abstand zwischen A und B berechnen: d_AB=|$\overrightarrow{\mathrm{AB}}$| = $\sqrt{0^2+8^2+{\mathrm{(-6)}}^2}$ = 10

Für die Gerade durch A und B gilt:
g_AB: $\overrightarrow{x}$ = $\overrightarrow{\mathrm{OA}}$ + t ⋅ $\overrightarrow{\mathrm{AB}}$, also $\overrightarrow{x}=$ $\left(\begin{array}{c}-3\\ 0\\ 4\end{array}\right)+t\cdot \left(\begin{array}{c}0\\ 8\\ -6\end{array}\right)$

Da der gesuchte Abstand 20 gerade 2 mal so lang ist wie die Länge des Richtungsvektors $\left(\begin{array}{c}0\\ 8\\ -6\end{array}\right)$ (|$\overrightarrow{\mathrm{AB}}$|=10), muss für die Ortsvektoren der gesuchten Punkte gelten:

= $\overrightarrow{\mathrm{OA}}$ + 2 ⋅ $\overrightarrow{\mathrm{AB}}$ = $\left(\begin{array}{c}-3\\ 0\\ 4\end{array}\right)+2\cdot \left(\begin{array}{c}0\\ 8\\ -6\end{array}\right)$ = $\left(\begin{array}{c}-3\\ 16\\ -8\end{array}\right)$, also 2 in die Geradengleichung eingesetzt.

= $\overrightarrow{\mathrm{OA}}$ - 2 ⋅ $\overrightarrow{\mathrm{AB}}$ = $\left(\begin{array}{c}-3\\ 0\\ 4\end{array}\right)-2\cdot \left(\begin{array}{c}0\\ 8\\ -6\end{array}\right)$ = $\left(\begin{array}{c}-3\\ -16\\ 16\end{array}\right)$, also -2 in die Geradengleichung eingesetzt.

Die gesuchten Punkte sind also P₁$\left(-3|16|-8\right)$ und P₂$\left(-3|-16|16\right)$.