Man braucht einen Vektor $\left(\begin{array}{c}a\\ b\\ c\end{array}\right)$, für den $\left(\begin{array}{c}-5\\ 2\\ 2\end{array}\right)$⋅$\left(\begin{array}{c}a\\ b\\ c\end{array}\right)$=0 gilt. Hierfür gibt es unendlich viele richtige Lösungen. Eine mögliche wäre z.B. $\left(\begin{array}{c}2\\ 2\\ 3\end{array}\right)$, denn $\left(\begin{array}{c}-5\\ 2\\ 2\end{array}\right)$∘$\left(\begin{array}{c}2\\ 2\\ 3\end{array}\right)$=$\mathrm{(-5)}\cdot 2+2\cdot 2+2\cdot 3=-10\mathrm{+4}\mathrm{+6}=0$

Damit die beiden Geraden orthogonal sind, müssen deren Richtungsvektoren orthogonal sein. Wir suchen also einen Vektor, der orthogonal zum gegebenen Richtungsvektor $\left(\begin{array}{c}0\\ 1\\ -5\end{array}\right)$ ist.

Hierfür gibt es unendlich viele richtige Lösungen. Eine mögliche wäre z.B. $\left(\begin{array}{c}5\\ 5\\ 1\end{array}\right)$, denn $\left(\begin{array}{c}0\\ 1\\ -5\end{array}\right)$∘$\left(\begin{array}{c}5\\ 5\\ 1\end{array}\right)$=$0\cdot 5+1\cdot 5+\mathrm{(-5)}\cdot 1=0\mathrm{+5}-5=0$

Damit sich die beiden Geraden nun auch wirklich schneiden und nicht windschief sind, muss gewährleistet sein, dass die beiden Geraden einen gemeinsamen Punkt haben. Am einfachsten geht das, indem man der gesuchten orthogonalen Geraden einfach den selben Aufpunkt wie der der gegebenen Geraden verpasst.

Somit ergibt sich h:$\overrightarrow{x}=$ $\left(\begin{array}{c}-1\\ 2\\ -1\end{array}\right)+t\cdot \left(\begin{array}{c}5\\ 5\\ 1\end{array}\right)$ als eine möglich Lösung.

Man braucht eine Ebene, die orthogonal zur Ebene E ist, also müssen auch die beiden Normalenvektoren orthogonal sein.

Man braucht also einen Vektor der orthogonal zum Normalenvektor einer Ebene E: $\left(\begin{array}{c}5\\ -3\\ 1\end{array}\right)$ ist.

,

Hierfür gibt es unendlich viele richtige Lösungen. Eine mögliche wäre z.B. $\left(\begin{array}{c}1\\ 1\\ -2\end{array}\right)$, denn $\left(\begin{array}{c}5\\ -3\\ 1\end{array}\right)$∘$\left(\begin{array}{c}1\\ 1\\ -2\end{array}\right)$=$5\cdot 1+\mathrm{(-3)}\cdot 1+1\cdot \mathrm{(-2)}=5-3-2=0$

Eine mögliche Ebene wäre also $\mathrm{}{x}_1+x_2-2x_3=\mathrm{d}$

Über den Wert auf der rechten Seite braucht man sich keine Gedanken zu machen, weil ja alle Ebenen mit dem gleichen Normalenvektor immer parallel zueinander sind, unabhängig von dem d auf der rechten Seite. Wenn also eine der Ebenen orthogonal zur gesuchten Ebene ist, so ist es jede. Deswegen nehmen wir für das d auf der rechten Seite einfach 0.

Eine mögliche Ebene wäre also E:$\mathrm{}{x}_1+x_2-2x_3=0$

Wir berechnen zuerst einmal die drei Verbindungsvektoren jeweils zwischen zwei Punkten:

$\overrightarrow{\mathrm{AB}}$ = $\left(\begin{array}{c}-1\\ 0\\ 4\end{array}\right)$, $\overrightarrow{\mathrm{AC}}$ = $\left(\begin{array}{c}-1\\ -5\\ -1\end{array}\right)$ und $\overrightarrow{\mathrm{BC}}$ = $\left(\begin{array}{c}0\\ -5\\ -5\end{array}\right)$

Jetzt schauen wir uns die Längen der drei Vektoren an:

|$\overrightarrow{\mathrm{AB}}$| = $\sqrt{{\mathrm{(-1)}}^2+0^2+4^2}=\sqrt{17}$

|$\overrightarrow{\mathrm{AC}}$| = $\sqrt{{\mathrm{(-1)}}^2+{\mathrm{(-5)}}^2+{\mathrm{(-1)}}^2}=\sqrt{27}$

|$\overrightarrow{\mathrm{BC}}$| = $\sqrt{0^2+{\mathrm{(-5)}}^2+{\mathrm{(-5)}}^2}=\sqrt{50}$

Da alle drei Vektor- und damit Seitenlängen verschieden lang sind, ist das Dreieck nicht gleichschenklig.

Jetzt untersuchen wir die drei Vektoren paarweise auf Orthogonalität:

$\overrightarrow{\mathrm{AB}}$⋅$\overrightarrow{\mathrm{AC}}$ = $\left(\begin{array}{c}-1\\ 0\\ 4\end{array}\right)$∘$\left(\begin{array}{c}-1\\ -5\\ -1\end{array}\right)$=$\mathrm{(-1)}\cdot \mathrm{(-1)}+0\cdot \mathrm{(-5)}+4\cdot \mathrm{(-1)}=1\mathrm{+0}-4=-3$

$\overrightarrow{\mathrm{AB}}$⋅$\overrightarrow{\mathrm{BC}}$ = $\left(\begin{array}{c}-1\\ 0\\ 4\end{array}\right)$∘$\left(\begin{array}{c}0\\ -5\\ -5\end{array}\right)$=$\mathrm{(-1)}\cdot 0+0\cdot \mathrm{(-5)}+4\cdot \mathrm{(-5)}=0\mathrm{+0}-20=-20$

$\overrightarrow{\mathrm{BC}}$⋅$\overrightarrow{\mathrm{AC}}$ = $\left(\begin{array}{c}0\\ -5\\ -5\end{array}\right)$∘$\left(\begin{array}{c}-1\\ -5\\ -1\end{array}\right)$=$0\cdot \mathrm{(-1)}+\mathrm{(-5)}\cdot \mathrm{(-5)}+\mathrm{(-5)}\cdot \mathrm{(-1)}=0\mathrm{+25}\mathrm{+5}=30$

Da alle drei Skalarprodukte ungleich 0 sind, sind alle drei Winkel ungleich 90°, das Dreieck ist also nicht rechtwinklig.

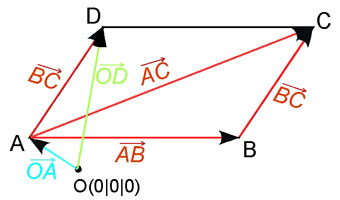Wir sehen in der Skizze, dass man den Verbindungsvektor zwischen B und C, also
$\overrightarrow{\mathrm{BC}}$ = = $\left(\begin{array}{c}4\\ 0\\ -2\end{array}\right)$
zum Ortsvektor von A addieren muss, um den Ortsvektor von D zu erhalten:

$\overrightarrow{\mathrm{OD}}$ = $\overrightarrow{\mathrm{OA}}$ + $\overrightarrow{\mathrm{BC}}$ = $\left(\begin{array}{c}1\\ 5\\ -5\end{array}\right)$ + $\left(\begin{array}{c}4\\ 0\\ -2\end{array}\right)$ = $\left(\begin{array}{c}5\\ 5\\ -7\end{array}\right)$

Der gesuchte 4. Punkt ist also D$\left(5|5|-7\right)$

Jetzt muss noch überprüft werden, ob dieses Parallelogramm eine spezielles ist:

Dazu überprüfen wir zuerst, ob ein rechter Winkel in diesem Parallelogramm ist. Es genügt hier zu prüfen, ob ein rechter Winkel in B ist, weil ein Parallelogramm entweder nur rechte Winkel oder eben keinen hat. (Ein rechter Winkel zwischen $\overrightarrow{\mathrm{AB}}$ und $\overrightarrow{\mathrm{AC}}$ ist unerheblich, da ja $\overrightarrow{\mathrm{AC}}$ inzwischen die Diagonale des Parallelogramms ist).

Wir untersuchen also das Skalarprodukt von $\overrightarrow{\mathrm{AB}}$= = $\left(\begin{array}{c}-3\\ 1\\ -6\end{array}\right)$ und $\overrightarrow{\mathrm{BC}}$, also
$\overrightarrow{\mathrm{AB}}$ ⋅ $\overrightarrow{\mathrm{BC}}$ = $\left(\begin{array}{c}-3\\ 1\\ -6\end{array}\right)$∘$\left(\begin{array}{c}4\\ 0\\ -2\end{array}\right)$=$\mathrm{(-3)}\cdot 4+1\cdot 0+\mathrm{(-6)}\cdot \mathrm{(-2)}=-12\mathrm{+0}\mathrm{+12}=0$

Da das Skalarprodukt gleich 0 ist, sind die beiden Vektoren orthogonal und das Parallelogramm ist ein Rechteck.

Jetzt muss noch untersucht werden, ob die beiden nicht gegenüberliegenden Seiten des Parallelogramms gleich lang sind. Dazu berechnen wir einfach die Beträge der beiden Vektoren $\overrightarrow{\mathrm{AB}}$ und $\overrightarrow{\mathrm{BC}}$:

|$\overrightarrow{\mathrm{AB}}$| = $\sqrt{{\mathrm{(-3)}}^2+1^2+{\mathrm{(-6)}}^2}=\sqrt{46}$

|$\overrightarrow{\mathrm{BC}}$| = $\sqrt{4^2+0^2+{\mathrm{(-2)}}^2}=\sqrt{20}$

Da die beiden Vektoren verschiedene Längen haben, ist das Parallelogramm keine Raute.

Man braucht eine Ebene, in der die Gerade g liegt. Da der Normalenvektoren immer orthogonal zur Ebene ist, muss dieser in diesem Fall auch orthogonal zur Geraden, also zu deren Richtungsvektor $\left(\begin{array}{c}-1\\ 0\\ -4\end{array}\right)$ sein.

Hierfür gibt es unendlich viele richtige Lösungen. Eine mögliche wäre z.B. $\left(\begin{array}{c}4\\ 4\\ -1\end{array}\right)$, denn $\left(\begin{array}{c}-1\\ 0\\ -4\end{array}\right)$∘$\left(\begin{array}{c}4\\ 4\\ -1\end{array}\right)$=$\mathrm{(-1)}\cdot 4+0\cdot 4+\mathrm{(-4)}\cdot \mathrm{(-1)}=-4\mathrm{+0}\mathrm{+4}=0$

Eine mögliche Ebene wäre also $4x_1+4x_2-x_3=\mathrm{d}$

Damit die Ebene nun nicht parallel zu g liegt, muss gewährleistet sein, dass ein Punkt von g (und damit automatisch alle) in der Ebene liegt. Dazu setzen wir den Aufpunkt $\left(2|3|5\right)$ in die Ebenengleichung ein und erhalten somit den richtigen Wert für d: $4\cdot 2+4\cdot 3+\mathrm{(-1)}\cdot 5$ = 15 = d

Ein mögliche Ebene wäre also E:$4x_1+4x_2-x_3=15$

Man braucht eine Ebene, die orthogonal zur Gerade g, also zu deren Richtungsvektor $\overrightarrow{u}$=$\left(\begin{array}{c}0\\ -1\\ 0\end{array}\right)$ ist.

Da der Normalenvektor einer Ebene ja auch immer orthogonal zu seiner Ebene ist, kann man also den Richtungsvektor oder ein Vielfaches von diesem als Normalenvektor nehmen.

Den Wert rechts vom Gleichheitszeichen kann man beliebig wählen, da dieser nur bestimmt wo, aber nicht wie die Ebene im Raum liegt.

Eine mögliche Ebene wäre also E:$-x_2=0$

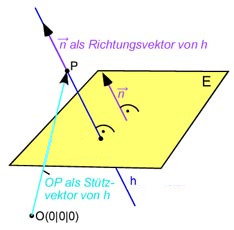
Wenn h orthogonal zur Ebene E sein soll, so kann man als Richtungsverktor von h den Normalenvektor $\overrightarrow{n}$=$\left(\begin{array}{c}-2\\ 9\\ 0\end{array}\right)$ der Ebene E verwenden.

Da der Punkt P$\left(-3|-3|4\right)$ auf der gesuchten Geraden liegen soll, können wir diesen einfach als Stützvektor der gesuchten Gerdaen verwenden.

Somit ergibt sich für die gesuchte Gerade die Gleichung g: $\overrightarrow{x}=$ $\left(\begin{array}{c}-3\\ -3\\ 4\end{array}\right)+t\cdot \left(\begin{array}{c}-2\\ 9\\ 0\end{array}\right)$.

Man braucht eine Ebene, die parallel zur Geraden g ist. Da der Normalenvektoren immer orthogonal zur Ebene ist, muss dieser in diesem Fall auch orthogonal zur Geraden, also zu deren Richtungsvektor $\left(\begin{array}{c}-3\\ 0\\ 0\end{array}\right)$ sein.

Hierfür gibt es unendlich viele richtige Lösungen. Eine mögliche wäre z.B. $\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$, denn $\left(\begin{array}{c}-3\\ 0\\ 0\end{array}\right)$∘$\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$=$\mathrm{(-3)}\cdot 0+0\cdot 0+0\cdot 1=0\mathrm{+0}\mathrm{+0}=0$

Daraus ergibt sich eine mögliche Ebene E:$+x_3=0$

Man braucht eine Gerade, die parallel zur Ebene E ist. Da der Normalenvektor $\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)$ orthogonal zur Ebene ist, muss dieser also auch orthogonal zur gesuchten Gerade, un damit zu dessen Richtungsvektor sein.

Hierfür gibt es unendlich viele richtige Lösungen. Eine mögliche wäre z.B. $\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$, denn $\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)$∘$\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$=$0\cdot 0+1\cdot 0+0\cdot 1=0\mathrm{+0}\mathrm{+0}=0$

Eine mögliche Gerade wäre also g:$\overrightarrow{x}=$ $\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)+t\cdot \left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$

Man braucht eine Ebene, die orthogonal zur Gerade g, also zu deren Richtungsvektor $\overrightarrow{u}$=$\left(\begin{array}{c}-1\\ 4\\ 1\end{array}\right)$ ist.

Da der Normalenvektor einer Ebene ja auch immer orthogonal zu seiner Ebene ist, kann man also den Richtungsvektor oder ein Vielfaches von diesem als Normalenvektor nehmen.

Den Wert rechts vom Gleichheitszeichen kann man beliebig wählen, da dieser nur bestimmt wo, aber nicht wie die Ebene im Raum liegt.

Eine mögliche Ebene wäre also E:$\mathrm{-}{x}_1+4x_2+x_3=0$