Mathebattle EduRandomtasks

nach Aufgabentypen suchen

Aufgabentypen anhand von Beispielen durchstöbern

Browserfenster aktualisieren (F5), um neue Beispiele bei den Aufgabentypen zu sehen

2. Strahlensatz (gleiche Seite)

Beispiel:

Die beiden blauen Geraden sind parallel.
Berechne x.

Lösung einblenden

Nach dem 2. Strahlensatz gilt:

$\frac{x}{8}$ = $\frac{9 + 9}{9}$

$\frac{x}{8}$	=	$\frac{9}{9} + \frac{9}{9}$
$\frac{1}{8} x$	=	$1 + 1$
$\frac{1}{8} x$	=	$2$	\|⋅ 8
$x$	=	$16$

2. Strahlensatz (2 Seiten)

Beispiel:

Die beiden blauen Geraden sind parallel.
Berechne x.

Lösung einblenden

Nach dem 2. Strahlensatz gilt:

$\frac{x}{8}$ = $\frac{27}{9}$

$\frac{x}{8}$	=	$\frac{27}{9}$
$\frac{1}{8} x$	=	$3$	\|⋅ 8
$x$	=	$24$

2. Strahlensatz (3 Segmente)

Beispiel:

Die blauen Geraden sind parallel.
Berechne x und y.

Lösung einblenden

Wir betrachten zuerst den Teil rechts vom Zentrum.

Nach dem 2. Strahlensatz gilt:

$\frac{x}{15}$ = $\frac{8}{8 + 22}$

$\frac{x}{15}$	=	$\frac{4}{15}$
$\frac{1}{15} x$	=	$\frac{4}{15}$	\|⋅ 15
$x$	=	$4$

Nun betrachten wir den Teil links vom Zentrum.

Nach dem 2. Strahlensatz gilt:

$\frac{y}{4}$ = $\frac{16}{8}$

$\frac{y}{4}$	=	$\frac{16}{8}$
$\frac{1}{4} y$	=	$2$	\|⋅ 4
$y$	=	$8$

doppelter Strahlensatz (klein)

Beispiel:

Die beiden blauen Geraden sind parallel.
Berechne x und y.

Lösung einblenden

Nach dem 1. Strahlensatz gilt:

$\frac{x + 18}{x}$ = $\frac{9 + 16,2}{9}$

D=R\{0}

$\frac{x}{x} + \frac{18}{x}$	=	$\frac{9}{9} + \frac{16,2}{9}$
$1 + \frac{18}{x}$	=	$2,8$

Wir multiplizieren den Nenner $x$ weg!

$1 + \frac{18}{x}$	=	$2,8$	\|⋅( $x$ )
$1 \cdot x + \frac{18}{x} \cdot x$	=	$2,8 \cdot x$
$x + 18$	=	$2,8 x$

$x + 18$	=	$2,8 x$	\| $- 18$ $- 2,8 x$
$- 1,8 x$	=	$- 18$	\|:( $- 1,8$ )
$x$	=	$10$

(Alle Lösungen sind auch in der Definitionsmenge).

Nach dem 2. Strahlensatz gilt:

$\frac{y}{8}$ = $\frac{10 + 18}{10}$

$\frac{y}{8}$	=	$\frac{10}{10} + \frac{18}{10}$
$\frac{1}{8} y$	=	$1 + \frac{9}{5}$
$\frac{1}{8} y$	=	$\frac{14}{5}$	\|⋅ 8
$y$	=	$\frac{112}{5}$ = 22.4

Strahlensatz Anwendungen

Beispiel:

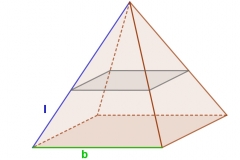
Die Grundfläche einer senkrechten quadratischen Pyramide ist b=38,4 m lang. Parallel zur Grundfläche wird eine zweite Ebene eingezogen, deren Grundfläche ein Quadrat mit Seitenlänge 16 m ist. Die Kantenlänge des oberen pyramidenformigen Stocks beträgt 6 m. Bestimme die Kantenlänge des unteren Stockwerks (in Form eines Pyramidenstumpfs).

Lösung einblenden

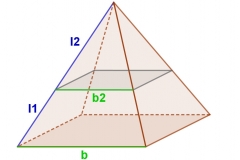
Wenn man in die Skizze ein paar Strecken einzeichnet, erkennt man eine Strahlensatzfigur:

Dabei gilt nach dem 2. Strahlensatz:

$\frac{b}{b2}$ = $\frac{l2+l1}{l2}$ bzw. $\frac{b2}{b}$ = $\frac{l2}{l2+l1}$

Aus dem Text können wir herauslesen:

l2 = 6

b2 = 16

b = 38.4

Gesucht ist die Kantenlänge des unteren Stocks der Pyramide. Wir wählen also l1 als x.

Jetzt können wir die Werte in die obige Strahlensatzgleichung einsetzen und erhalten:

$\frac{6 + x}{6}$ = $\frac{38,4}{16}$

$\frac{6}{6} + \frac{x}{6}$	=	$\frac{38,4}{16}$
$1 + \frac{1}{6} x$	=	$\frac{38,4}{16}$
$\frac{1}{6} x + 1$	=	$2,4$	\|⋅ 6
$6 (\frac{1}{6} x + 1)$	=	$14,4$
$x + 6$	=	$14,4$	\| $- 6$
$x$	=	$8,4$

l1 ist also $8,4$ .

Die Lösung ist somit: 8.4