 Klasse 5-6
Klasse 5-6
 Klasse 7-8
Klasse 7-8
 Klasse 9-10
Klasse 9-10
 Kursstufe
Kursstufe
 cosh
cosh
nach Aufgabentypen suchen
Aufgabentypen anhand von Beispielen durchstöbern
Browserfenster aktualisieren (F5), um neue Beispiele bei den Aufgabentypen zu sehen
Koordinatenform aus der Parameterform aufstellen
Beispiel:
Stelle eine Koordinatengleichung der Ebene mit der Parametergleichung
auf!
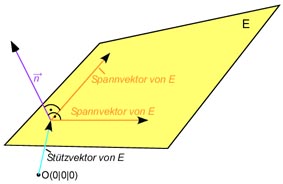 Wir berechnen einen Normalenvektor, der senkrecht zu den beiden Spannvektoren steht:
Wir berechnen einen Normalenvektor, der senkrecht zu den beiden Spannvektoren steht:
Weil beim Vektor in der x3-Koordinate eine 0 steht, wäre ja der Vektor für jedes t orthogonal
zu , denn
Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Vektor ⋅ =
14⋅t
Der gesuchte Normalenvektor ist also = = ⋅
Alternativ dazu hätte man auch das Vektorprodukt (Kreuzprodukt) berechnen können:
= 7⋅Weil der Vektor orthogonal zu und , also orthogonal zur Ebene und damit zu jedem Vektor in der Ebene ist,
gilt die Normalengleichung der Ebene:
Unsere Ebenengleichung in Koordinatenform ist also
Durch Einsetzen des Aufpunktes der Ebene A erhält man
d =
also:
Koordinatenform aus 3 Punkten aufstellen
Beispiel:
Stelle eine Koordinatengleichung der Ebene durch die Punkte P1, P2 und P3 auf!
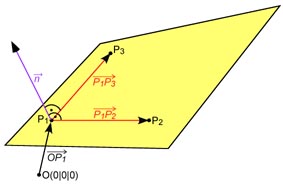 Wir nehmen den Ortsvektor des ersten Punkts als Stützvektor.
Die Verbindungsvektoren zwischen 1. und 2. bzw. zwischen 1. und 3. Punkt bilden die beiden Spannvektoren.
Die Parametergleichung der Ebene ist also:
Wir nehmen den Ortsvektor des ersten Punkts als Stützvektor.
Die Verbindungsvektoren zwischen 1. und 2. bzw. zwischen 1. und 3. Punkt bilden die beiden Spannvektoren.
Die Parametergleichung der Ebene ist also:.
Wir berechnen einen Normalenvektor, der senkrecht zu den beiden Spannvektoren steht:
Weil beim Vektor in der x3-Koordinate eine 0 steht, wäre ja der Vektor für jedes t orthogonal
zu , denn
Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Vektor ⋅ =
-11⋅t
Der gesuchte Normalenvektor ist also =
Alternativ dazu hätte man auch das Vektorprodukt (Kreuzprodukt) berechnen können:
= 11⋅Weil der Vektor orthogonal zu und , also orthogonal zur Ebene und damit zu jedem Vektor in der Ebene ist,
gilt die Normalengleichung der Ebene:
Unsere Ebenengleichung in Koordinatenform ist also
Durch Einsetzen des Aufpunktes der Ebene A erhält man
d =
also:
Koordinatenform aus einem Punkt und einer Geraden
Beispiel:
Stelle eine Koordinatengleichung der Ebene durch den Punkt P1 und die Gerade g: auf!
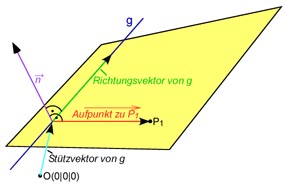 Wir nehmen den Stützvektor der Geraden als Stützvektor der Ebene
und den Richtungsvektor der Geraden als einen Spannvektor. Als anderen Spannvektor nehmen wir den
Verbindungsvektor zwischen dem gegebenen Punkt und dem Aufpunkt der Geraden:
Wir nehmen den Stützvektor der Geraden als Stützvektor der Ebene
und den Richtungsvektor der Geraden als einen Spannvektor. Als anderen Spannvektor nehmen wir den
Verbindungsvektor zwischen dem gegebenen Punkt und dem Aufpunkt der Geraden:
- =
Wir erhalten so also eine Parametergleichung der Ebene:
Wir berechnen einen Normalenvektor, der senkrecht zu den beiden Spannvektoren steht:Weil beim Vektor in der x2-Koordinate eine 0 steht, wäre ja der Vektor für jedes t orthogonal
zu , denn
Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Vektor ⋅ =
-3⋅t
Der gesuchte Normalenvektor ist also = = ⋅
Alternativ dazu hätte man auch das Vektorprodukt (Kreuzprodukt) berechnen können:
Weil der Vektor orthogonal zu und , also orthogonal zur Ebene und damit zu jedem Vektor in der Ebene ist,
gilt die Normalengleichung der Ebene:
Unsere Ebenengleichung in Koordinatenform ist also
Durch Einsetzen des Aufpunktes der Ebene A erhält man
d =
also:
Koordinatenform aus 2 parallelen Geraden
Beispiel:
Stelle eine Koordinatengleichung der Ebene auf, die von den beiden parallelen Geraden g: und h: aufgespannt wird!
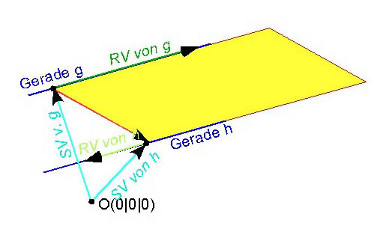 Wir nehmen den Stützvektor
der einen Geraden als Stützvektor der Ebene und den Richtungsvektor der gleichen Geraden als einen Spannvektor.
Den Richtungsvektor der anderen Geraden können wir leider nicht als weiteren Spannvektor nehmen, da dieser ja in die gleiche
Richtung zeigt wie der der anderen Geraden. Der Verbindungsvektor der beiden Aufpunkte
liegt aber auch in der Ebene, die von den beiden parallelen Geraden aufgespannt wird.
Deswegen nehmen wir diesen als zweiten Spannvektor:
Wir nehmen den Stützvektor
der einen Geraden als Stützvektor der Ebene und den Richtungsvektor der gleichen Geraden als einen Spannvektor.
Den Richtungsvektor der anderen Geraden können wir leider nicht als weiteren Spannvektor nehmen, da dieser ja in die gleiche
Richtung zeigt wie der der anderen Geraden. Der Verbindungsvektor der beiden Aufpunkte
liegt aber auch in der Ebene, die von den beiden parallelen Geraden aufgespannt wird.
Deswegen nehmen wir diesen als zweiten Spannvektor:Wir berechnen einen Normalenvektor, der senkrecht zu den beiden Spannvektoren steht:
Weil beim Vektor in der x3-Koordinate eine 0 steht, wäre ja der Vektor für jedes t orthogonal
zu , denn
Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Vektor ⋅ =
-3⋅t
Der gesuchte Normalenvektor ist also =
Alternativ dazu hätte man auch das Vektorprodukt (Kreuzprodukt) berechnen können:
= 3⋅Weil der Vektor orthogonal zu und , also orthogonal zur Ebene und damit zu jedem Vektor in der Ebene ist,
gilt die Normalengleichung der Ebene:
Unsere Ebenengleichung in Koordinatenform ist also
Durch Einsetzen des Aufpunktes der Ebene A erhält man
d =
also:
Koordinatenform aus 3 Punkten aufstellen
Beispiel:
Stelle eine Koordinatengleichung der Ebene durch die Punkte P1, P2 und P3 auf!
 Wir nehmen den Ortsvektor des ersten Punkts als Stützvektor.
Die Verbindungsvektoren zwischen 1. und 2. bzw. zwischen 1. und 3. Punkt bilden die beiden Spannvektoren.
Die Parametergleichung der Ebene ist also:
Wir nehmen den Ortsvektor des ersten Punkts als Stützvektor.
Die Verbindungsvektoren zwischen 1. und 2. bzw. zwischen 1. und 3. Punkt bilden die beiden Spannvektoren.
Die Parametergleichung der Ebene ist also:.
Wir berechnen einen Normalenvektor, der senkrecht zu den beiden Spannvektoren steht:
Weil beim Vektor in der x1-Koordinate eine 0 steht, wäre ja der Vektor für jedes t orthogonal
zu , denn
Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Vektor ⋅ =
-4⋅t
Der gesuchte Normalenvektor ist also =
Alternativ dazu hätte man auch das Vektorprodukt (Kreuzprodukt) berechnen können:
= 4⋅Weil der Vektor orthogonal zu und , also orthogonal zur Ebene und damit zu jedem Vektor in der Ebene ist,
gilt die Normalengleichung der Ebene:
Unsere Ebenengleichung in Koordinatenform ist also
Durch Einsetzen des Aufpunktes der Ebene A erhält man
d =
also:
Koordinatenform aus Normalengleichung
Beispiel:
Bestimme eine Koordinatengleichung der Ebene E :
⇔
⇔ ∘ - ∘ = 0
⇔ - () = 0
⇔
⇔
