 Klasse 5-6
Klasse 5-6
 Klasse 7-8
Klasse 7-8
 Klasse 9-10
Klasse 9-10
 Kursstufe
Kursstufe
 cosh
cosh
nach Aufgabentypen suchen
Aufgabentypen anhand von Beispielen durchstöbern
Browserfenster aktualisieren (F5), um neue Beispiele bei den Aufgabentypen zu sehen
Graph-Term-Zuordnung BF
Beispiel:
Ordne die Funktionen den Graphen zu.
f(x)=
g(x)=
h(x)=
i(x)=
Zu Graph Nr. 1:
Der Graph von hat im Bereich für negative x keine Funktionswerte. Er steigt zunächst sehr schnell, dann nimmt die Steigung aber ab. Er sieht aus wie eine halbe Parabel, die um 90° gedreht wurde. Er besitzt die Punkte (0|0), (1|1), (4|2), usw.Der Graph Nr. 1 gehört also zur Funktion g(x) = .
Zu Graph Nr. 2:
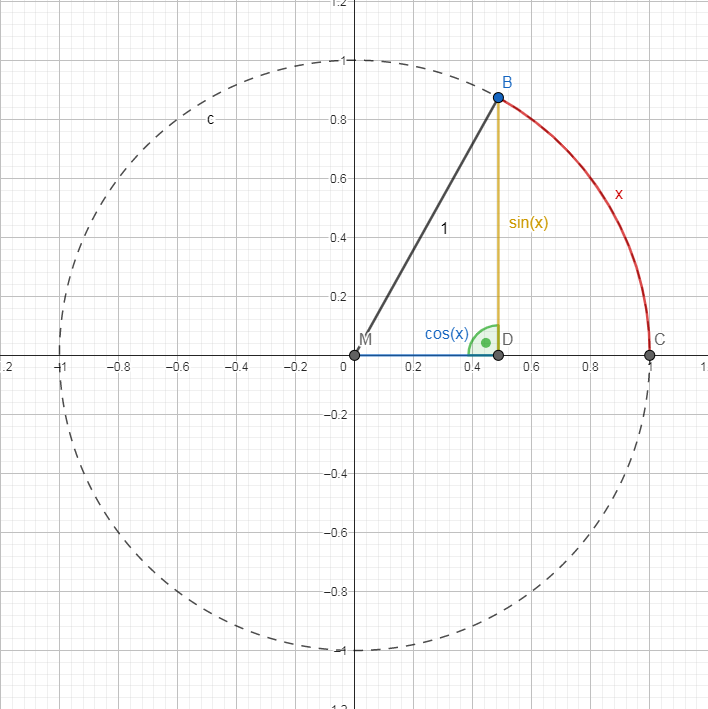 Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann:
Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann: Der Graph Nr. 2 gehört also zur Funktion h(x) = .
Zu Graph Nr. 3:
Den Graph von erkennt man an seinem Sattelpunkt und der immer größer werdenden Steigung, je weiter sich der Graph vom Ursprung entfernt. Er besitzt die Punkte (-2|-8), (-1|1), (0|0), (1|1), (2|8), usw.Der Graph Nr. 3 gehört also zur Funktion i(x) = .
Zu Graph Nr. 4:
Den Graph von erkennt man an den Asymptoten an den beiden Achsen. Es handelt sich um eine Hyperbel. Je näher x an 0 kommt, umso betragsmäßig größer wird der Funktionswert (weil ja x im Nenner steht). Je weiter x sich von 0 entfernt, umso betragsmäßig kleiner wird der Funktionswert, weil ja der Nenner immer größer wird. Der Graph verläuft durch die Punkte (1|1) und (-1|-1), weil f(1) = = 1 und f(-1) = = -1. Im Gegensatz zu hat er für negative x-Werte negative Funktionswerte und für positive x-Werte positive Funktionswerte.Der Graph Nr. 4 gehört also zur Funktion f(x) = .
Graph-Term-Zuordnung LF
Beispiel:
Ordne die Funktionen den Graphen zu.
f(x)=
g(x)=
h(x)=
i(x)=
Zu Graph Nr. 1:
 Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann:
Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann: Der Graph Nr. 1 gehört also zur Funktion g(x) = .
Zu Graph Nr. 2:
Der Graph von hat im Bereich für negative x keine Funktionswerte. Er steigt zunächst sehr schnell, dann nimmt die Steigung aber ab. Er sieht aus wie eine halbe Parabel, die um 90° gedreht wurde. Er besitzt die Punkte (0|0), (1|1), (4|2), usw.Der Graph Nr. 2 gehört also zur Funktion f(x) = .
Zu Graph Nr. 3:
Den Graph von erkennt man an seinem Sattelpunkt und der immer größer werdenden Steigung, je weiter sich der Graph vom Ursprung entfernt. Er besitzt die Punkte (-2|-8), (-1|1), (0|0), (1|1), (2|8), usw.Der Graph Nr. 3 gehört also zur Funktion i(x) = .
Zu Graph Nr. 4:
Den Graph von erkennt man an den Asymptoten an den beiden Achsen. Es handelt sich um eine Hyperbel. Je näher x an 0 kommt, umso größer wird der Funktionswert. Je weiter x sich von 0 entfernt, umso kleiner wird der Funktionswert (weil ja x im Nenner steht). Im Gegensatz zu hat er sowohl für negative, als auch für positive x positive Funktionswerte. Er ist also achsensymmetrisch bzgl. der y-Achse und enthält z.B. die Punkte (1|1) und (-1|1).Der Graph Nr. 4 gehört also zur Funktion h(x) = .
Graph-Term-Zuordnung 2 BF
Beispiel:
Ordne die Funktionen den Graphen zu.
f(x)=
g(x)=
h(x)=
i(x)=
j(x)=
k(x)=
Zu Graph Nr. 1:
 Der Graph von
schwingt zwischen 1 und -1. Im Gegensatz zum Sinus startet der Kosinus für x=0 bei 1 (cos(0)=1). Im Einheitskreis rechts wird dies deutlich:
Der Graph von
schwingt zwischen 1 und -1. Im Gegensatz zum Sinus startet der Kosinus für x=0 bei 1 (cos(0)=1). Im Einheitskreis rechts wird dies deutlich:
Der Graph Nr. 1 gehört also zur Funktion h(x) = .
Zu Graph Nr. 2:
Der Graph von nähert sich für negative x-Werte der x-Achse an und wächst für positive x-Werte sehr schnell. Er schneidet die y-Achse im Punkt (0|1), da = 1.Der Graph Nr. 2 gehört also zur Funktion k(x) = .
Zu Graph Nr. 3:
Den Graph von erkennt man an den Asymptoten an den beiden Achsen. Es handelt sich um eine Hyperbel. Je näher x an 0 kommt, umso betragsmäßig größer wird der Funktionswert (weil ja x im Nenner steht). Je weiter x sich von 0 entfernt, umso betragsmäßig kleiner wird der Funktionswert, weil ja der Nenner immer größer wird. Der Graph verläuft durch die Punkte (1|1) und (-1|-1), weil f(1) = = 1 und f(-1) = = -1. Im Gegensatz zu hat er für negative x-Werte negative Funktionswerte und für positive x-Werte positive Funktionswerte.Der Graph Nr. 3 gehört also zur Funktion f(x) = .
Zu Graph Nr. 4:
Der Graph von hat die typische Form einer nach oben geöffneten Normalparabel. Sie hat ihren Scheitel (Tiefpunkt) im Ursprung. Die Steigung wird vom Betrag immer größer, je weiter der Graph sich vom Ursprung entfernt. Besonders markant sind die Punkte (1|1), (2|4), usw.Der Graph Nr. 4 gehört also zur Funktion i(x) = .
Graph-Term-Zuordnung 2 LF
Beispiel:
Ordne die Funktionen den Graphen zu.
f(x)=
g(x)=
h(x)=
i(x)=
j(x)=
k(x)=
Zu Graph Nr. 1:
 Der Graph von
schwingt zwischen 1 und -1. Im Gegensatz zum Sinus startet der Kosinus für x=0 bei 1 (cos(0)=1). Im Einheitskreis rechts wird dies deutlich:
Der Graph von
schwingt zwischen 1 und -1. Im Gegensatz zum Sinus startet der Kosinus für x=0 bei 1 (cos(0)=1). Im Einheitskreis rechts wird dies deutlich:
Der Graph Nr. 1 gehört also zur Funktion h(x) = .
Zu Graph Nr. 2:
Der Graph von besitzt für negative x-Werte keine Funktionswerte, weil man den Logarithmus nur aus positiven Zahlen ziehen kann. Für x → 0 streben die y-Werte gegen -∞. Der Graph nähert sich somit der negativen y-Achse asymptotisch an. Für positive x-Werte steigt er sehr langsam an. Er schneidet die x-Achse im Punkt (1|0), da = 1 und somit = 0 ist.Der Graph Nr. 2 gehört also zur Funktion g(x) = .
Zu Graph Nr. 3:
Den Graph von erkennt man an den Asymptoten an den beiden Achsen. Es handelt sich um eine Hyperbel. Je näher x an 0 kommt, umso größer wird der Funktionswert. Je weiter x sich von 0 entfernt, umso kleiner wird der Funktionswert (weil ja x im Nenner steht). Im Gegensatz zu hat er sowohl für negative, als auch für positive x positive Funktionswerte. Er ist also achsensymmetrisch bzgl. der y-Achse und enthält z.B. die Punkte (1|1) und (-1|1).Der Graph Nr. 3 gehört also zur Funktion j(x) = .
Zu Graph Nr. 4:
Der Graph von nähert sich für negative x-Werte der x-Achse an und wächst für positive x-Werte sehr schnell. Er schneidet die y-Achse im Punkt (0|1), da = 1.Der Graph Nr. 4 gehört also zur Funktion i(x) = .
Graph-Term-Zuordn BF + Transf.
Beispiel:
Ordne die Funktionen den Graphen zu.
f(x)=
g(x)=
h(x)=
i(x)=
j(x)=
k(x)=
Zu Graph Nr. 1:
 Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann:
Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann: Am Graph Nr. 1 kann man all diese Eigenschaften erkennen, außer dass eben alle Punkte des Graphen noch zusätzlich um 1 in y-Richtung verschoben wurden.
Der Graph Nr. 1 gehört also zur Funktion f(x) = .
Zu Graph Nr. 2:
 Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann:
Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann: Der Graph Nr. 2 gehört also zur Funktion k(x) = .
Zu Graph Nr. 3:
 Der Graph von
schwingt zwischen 1 und -1. Im Gegensatz zum Sinus startet der Kosinus für x=0 bei 1 (cos(0)=1). Im Einheitskreis rechts wird dies deutlich:
Der Graph von
schwingt zwischen 1 und -1. Im Gegensatz zum Sinus startet der Kosinus für x=0 bei 1 (cos(0)=1). Im Einheitskreis rechts wird dies deutlich:Am Graph Nr. 3 kann man all diese Eigenschaften erkennen, außer dass eben alle Punkte des Graphen noch zusätzlich um 1 in y-Richtung verschoben wurden.
Der Graph Nr. 3 gehört also zur Funktion g(x) = .
Zu Graph Nr. 4:
 Der Graph von
schwingt zwischen 1 und -1. Im Gegensatz zum Sinus startet der Kosinus für x=0 bei 1 (cos(0)=1). Im Einheitskreis rechts wird dies deutlich:
Der Graph von
schwingt zwischen 1 und -1. Im Gegensatz zum Sinus startet der Kosinus für x=0 bei 1 (cos(0)=1). Im Einheitskreis rechts wird dies deutlich:
Der Graph Nr. 4 gehört also zur Funktion h(x) = .
Graph-Term-Zuordn LF + Transf.
Beispiel:
Ordne die Funktionen den Graphen zu.
f(x)=
g(x)=
h(x)=
i(x)=
j(x)=
k(x)=
Zu Graph Nr. 1:
 Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann:
Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann: Am Graph Nr. 1 kann man all diese Eigenschaften erkennen, außer dass eben alle Punkte des Graphen noch an der x-Achse gespiegelt wurden.
Der Graph Nr. 1 gehört also zur Funktion j(x) = .
Zu Graph Nr. 2:
 Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann:
Der Graph von
zwischen 1 und -1. Im Gegensatz zum Kosinus (cos(x)) startet der Sinus für x=0 im Ursprung O(0|0), was man am Einheitskreis rechts sehen kann: Der Graph Nr. 2 gehört also zur Funktion k(x) = .
Zu Graph Nr. 3:
Den Graph von erkennt man an den Asymptoten an den beiden Achsen. Es handelt sich um eine Hyperbel. Je näher x an 0 kommt, umso betragsmäßig größer wird der Funktionswert (weil ja x im Nenner steht). Je weiter x sich von 0 entfernt, umso betragsmäßig kleiner wird der Funktionswert, weil ja der Nenner immer größer wird. Der Graph verläuft durch die Punkte (1|1) und (-1|-1), weil f(1) = = 1 und f(-1) = = -1. Im Gegensatz zu hat er für negative x-Werte negative Funktionswerte und für positive x-Werte positive Funktionswerte.Der Graph Nr. 3 gehört also zur Funktion h(x) = .
Zu Graph Nr. 4:
Den Graph von erkennt man an seinem Sattelpunkt und der immer größer werdenden Steigung, je weiter sich der Graph vom Ursprung entfernt. Er besitzt die Punkte (-2|-8), (-1|1), (0|0), (1|1), (2|8), usw.Der Graph Nr. 4 gehört also zur Funktion f(x) = .
Ableitungen am Graph finden
Beispiel:
Gegeben ist eine Funktion f. Eine der 4 Abbildungen unten zeigt den Graph von f, eine andere zeigt den Graph der Ableitungsfunktion f'. Eine weitere Abbildung zeigt den Graph einer Stammfunktion F (von f). Die verbleibende vierte Abbildung zeigt den Graph einer ganz anderen Funktion g. Ordne die Graphen den Funktionen f, f', F und G zu
Als Vorgehensweise empfiehlt es sich, die markanten Punkte in Bezug auf die Ableitung, also Punkte mit waagrechter Tangente wie z.B. Hoch- und Tiefpunkte, bei den einzelnen Graphen zu betrachten.
Zu Graph Nr. 1:
Beim Graph Nr. 1 können wir bei x = -1 und bei x = -0.3 Punkte mit waagrechter Tangente erkennen.
Da ja genau an diesen Stellen der Graph 2 seine Nullstellen hat, könnte der Graph 2 die Ableitungsfunktion der Funktion vom Graph 1 zeigen.
Zu Graph Nr. 2:
Beim Graph Nr. 2 können wir bei x = -0.7 Punkte mit waagrechter Tangente erkennen.
Da ja genau an diesen Stellen der Graph 4 seine Nullstellen hat, könnte der Graph 4 die Ableitungsfunktion der Funktion vom Graph 2 zeigen.
Zu Graph Nr. 3:
Beim Graph Nr. 3 können wir bei x = -1, x = -0.5 und bei x = 0 Punkte mit waagrechter Tangente erkennen.
Zu Graph Nr. 4:
Beim Graph Nr. 4 können wir keine Punkte mit waagrechter Tangente finden.
Wir fassen also zusammen:
- Der Graph 2 zeigt die Ableitung vom Graph 1
- Der Graph 4 zeigt die Ableitung vom Graph 2
- Der Graph 3 scheint zu einer ganz anderen Funktion zu gehören.
Somit gilt:
Der Graph 1 gehört zur Funktion F(x).
Der Graph 2 gehört zur Funktion f(x).
Der Graph 3 gehört zur Funktion g(x).
Der Graph 4 gehört zur Funktion f '(x).
Term mit Eigenschaften finden
Beispiel:
Bestimme den Term einer Funktion, für dessen Graph folgende Bedingungen erfüllt sein müssen:
- gemeinsame Punkte mit der x-Achse: N1(-2|0) und N2(-1|0)
- Schnittpunkt mit der y-Achse: Sy(0|-4)
Als erstes stellen wir einen Term auf, der die geforderten Nullstellen besitzt. Dazu bekommt jede Nullstelle ihren Linearfaktor, also .
Um den y-Achsenabschnitt Sy(0|-4) zu überprüfen, setzen wir jetzt einfach x=0 in unseren bisherigen Term ein:
f(0) = =
Wir müssen somit unseren Term noch mit dem Koeffizienten multiplizieren, damit wir den gegebenen y-Achsenabschnit erhalten:
f(0) = =
Da also auch der y-Achsenabschnit passt, haben wir nun einen fertigen Funktionsterm .
Dieser funktionierende Term ist im roten Graphen eingezeichnet
Nullstellen und Faktorisieren
Beispiel:
Bestimme alle Nullstellen der Funktion f mit und gib f in Linearfaktordarstellung an.
Nullstellen sind die x-Werte, an denen der Funktionswert 0 beträgt, es muss also gelten:
f(x)=0
| = |
Diese Gleichung kann durch Substitution auf eine quadratische Gleichung zurückgeführt werden!
Setze u =
Draus ergibt sich die quadratische Gleichung:
= 0
Lösen mit der a-b-c-Formel (Mitternachtsformel):
eingesetzt in x1,2 = ergibt:
u1,2 =
u1,2 =
u1,2 =
u1 =
= =
u2 =
Lösen mit der p-q-Formel (x² + px + q = 0):
vor dem Einsetzen in x1,2 =
berechnen wir zuerst die Diskriminante D =
D =
x1,2 =
x1 =
x2 =
Rücksubstitution:
u1:
|
|
= | |
|
|
| x1 | = |
|
=
|
| x2 | = |
|
=
|
u2:
|
|
= | |
|
Diese Gleichung hat keine (reele) Lösung!
L={
Eine Mehrfachheit der Nullstellen muss natürlich auch in der faktorisierten Darstellung berücksichtigt werden.
Wenn wir den substituierten Term
Somit gilt für die faktorisierte Darstellung:
Schnittpkt-Anzahl in Abh. von Parameter
Beispiel:
Die Gerade y = m⋅x schneidet den Graph der Funktion f mit
Bestimme diese Werte von m.
An der Abbildung kann man erkennen, dass die Geraden, die den Graph von f berühren, der spannende Grenzfall sind.
Da ja y = m⋅x für jedes m immer durch den Ursprung O(0|0) verläuft, suchen wir also eine Tangente (von außen) an den Graphen von f durch den Ursprung:
Zuerst wird die Ableitung von f berechnet:
Wir kennen den Berührpunkt, in dem die gesuchte Tangente durch P(0|0) an das Schaubild von f angelegt wird, nicht. Deswegen nennen wir den x-Wert u. Der Funktionswert ist dann f(u), da der Berührpunkt ja auf dem Schaubild von f liegt. Außerdem muss die Ableitung in u ja gerade die Tangentensteigung sein, da B(u|f(u)) der Berührpunkt ist.
Wir können also P(0|0) als (x|y), den Berührpunkt B(u|f(u)) und m=f'(u)=
y=f´(u) ⋅(x-u)+f(u)
einsetzen:
0 =
Die Lösung der Gleichung:
|
|
= | ||
|
|
= |
Ein Produkt ist genau dann =0, wenn mindestens einer der beiden Faktoren =0 ist.
1. Fall:
|
|
= | |
|
|
| u1 | = |
2. Fall:
|
|
= | |
|
|
| u2 | = |
|
L={
Zusammenfassung:
Es gibt also insgesamt 2 Berührpunkte:
B(-1|-1.5)
B(0|0)
Um die Steigung der Tangente zu erhalten, setzen wir den gefundenen Wert x =
=
=
Man kann jetzt an der Abbildung gut erkennen, für m =
Wird die Gerade noch steiler als bei m =
Wird die Geraden weniger steil oder sogar positiv, also für also für alle
m <
Die richtige Lösung wäre hier also: m =
Parameter für Symmetrie finden
Beispiel:
Für welches a liegt beim Graph der Funktion fa mit
Gib die dann vorliegende Symmetrie an.
Man erkennt schnell, das keine Symmetrie zum Koordinatenssystem vorliegt, wenn nicht mindestens einer der Summanden von
Durch scharfes Hinsehen könnte man a = 2 erkennen. Man kann aber auch einfach bei jedem Summanden den Koeffizient anschauen und dann a so wählen, dass der Koeffizient = 0 wird:
-
( a - 1 ) x 4 ( 1 - 1 ) · x 4 + ( 1 - 2 ) · x 3 + 3 · x 2 + ( - 1 + 2 ) · x - x 3 + 3 x 2 + x -
( a - 2 ) x 3 ( 2 - 1 ) · x 4 + ( 2 - 2 ) · x 3 + 6 · x 2 + ( - 2 + 2 ) · x x 4 + 6 x 2 -
3 a x 2 ( 0 - 1 ) · x 4 + ( 0 - 2 ) · x 3 + 0 · x 2 + ( - 0 + 2 ) · x - x 4 - 2 x 3 + 2 x -
( - a + 2 ) x ( 2 - 1 ) · x 4 + ( 2 - 2 ) · x 3 + 6 · x 2 + ( - 2 + 2 ) · x x 4 + 6 x 2
Für a = 2 hat f2(x) =
Verschiebung Integral allg.
Beispiel:
Es gilt
Bestimme a, b und I.
Der Graph von f(x
Somit gilt a = -2 und b = 1.
Das
Anwendungen
Beispiel:
Ein Getränk wird aus dem Kühlschrank genommen und erwärmt sich. Die Temperatur des Getränks zur Zeit t kann für t ≥ 0 durch die Funktion f mit
- Bestimme die Temperatur des Getränks 2 Minuten nach Beobachtungsbeginn.
- Welche Temperatur hat das Getränk langfristig?
- Wann hat das Getränk die Temperatur von 44 erreicht?
- y-Wert bei t = 2
Gesucht ist der Funktionswert zur Zeit t=2. Wir berechnen also einfach f(2) =
45 - 30 e - 0,6 ⋅ 2 - 30 e - 1,2 + 45
- Verhalten für t gegen unendlich
Gesucht ist das Verhalten der Funktionswerte bei sehr großen t-Werten, also das Verhalten von f für t → ∞.
Für t → ∞ ⇒ f(t)=
45 - 30 e - 0,6 t 45 + 0 Das langfristige Verhalten der Funktionswerte geht also gegen
45 - Erster t-Wert bei y = 44
Gesucht sind die Zeitpunkte, an denen die Funktion die Werte y=44 annimmt.
Dazu setzen wir die Funktion einfach = 44 und lösen nach t auf:
45 - 30 e - 0,6 t = 44 - 30 e - 0,6 t + 45 = 44 | - 45 - 30 e - 0,6 t = - 1 |: - 30 e - 0,6 t = 1 30 |ln(⋅) - 0,6 t = ln ( 1 30 ) |: - 0,6 t = - 1 0,6 ln ( 1 30 ) ≈ 5.6687 Der erste Zeitpunkt an dem die die Funktion den Wert 44 annimmt, ist also nach 5.67 min.
