Mathebattle EduRandomtasks

Sinus und Thaleskreis (leicht)

Beispiel:

Das große Dreieck ist gleichschenklig.

Der blaue Halbkreis hat einen Durchmesser von u = 5.5 cm.

Die Länge der gemeinsamen Kante der beiden Dreiecke beträgt v = 4.6 cm.

Bestimme die fehlende Winkelweite α.

Lösung einblenden

Am blauen Thaleskreis erkennt man sofort, dass γ ein rechter Winkel sein muss.

Nach der Definition des Sinus gilt im rechtwinkligen Dreieck sin(β)= $\frac{Gegenkathete}{Hypotenuse}$

Damit folgt sin(β)= $\frac{4.6cm}{5.5cm}$ =0.836 und somit β=56.8°

Wegen der Winkelsumme im Dreieck muss gelten: 90° + β + φ = 180°.
Somit gilt φ = 90° - β° = 33.2°.

Wegen der Gleichschenkligkeit des großen Dreiecks muss nun aber β und (α+φ) gleich groß sein.

Mit α+33.2°=β=56.8° gilt nun: α = 23.5°

Sinus und Thaleskreis (schwer)

Beispiel:

Das große Dreieck ist gleichschenklig. Bestimme die Länge der Strecke PQ.

Lösung einblenden

Am blauen Thaleskreis über dem ersten Dreieck erkennt man sofort, dass γ ein rechter Winkel sein muss.

Als Nebenwinkel von γ muss natürluch auch δ ein recher Winkel sein.

Aufgrund der Winkelsumme im zweiten Dreieck folgt δ + ε + 40° = 180°.

Daraus folgt ε = 180° - 90° - 40° = 50°.

Mit Hilfe der Gleichschenkligkeit des großen Dreiecks kann mann nun β bestimmen: Es gilt ε + 2⋅β = 180°. Daraus folgt β = $\frac{180° - ε}{2}$ = $\frac{130°}{2}$ = 65°

Mit Hilfe des Sinus kann man nun die Länge der gemeinsamen Seite g der beiden Dreiecke berechnen:

Da g die Gegenkathete von β ist, gilt: sin(β)=sin(65°) = $\frac{g}{5.5cm}$

Damit folgt g = sin(65°) ⋅ 5.5cm ≈ 5cm

Nun können wir im zweiten Dreieck den Sinus anwenden und so die gesuchte Seite PQ herausfinden: sin(ε)= $\frac{g}{PQ}$

Setzt man die bekannten Werte ein, so folgt sin(50°)= $\frac{5}{PQ}$

Damit folgt: PQ = $\frac{5}{sin(50°)}$ = 6.5cm

Trigonometrie Anwendungen

Beispiel:

Von einem Fenster in 13m Höhe kann man den entfernten Rand eines Kanals unter dem Winkel α=70° gegenüber der Senkrechten betrachten. Der vordere Rand des Kanals erscheinet unter dem Winkel β=40° gegenüber der Senkrechten. Wie breit ist der Kanal?

Lösung einblenden

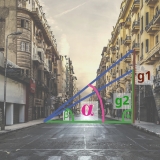
In beiden Dreiecken gilt für den Tangens: tan(α)= $\frac{Gegenkathete}{Ankathete}$ .
Da nach der Gegenkathete gesucht wird, stellen wir um zu
Gegenkathete g1=Ankathete ⋅ tan(α)=13 ⋅ tan(70°) ≈35.7172

Genau gleich verfahren wir mit dem anderen Dreieck:
Gegenkathete g2=Ankathete ⋅ tan(β)=13 ⋅ tan(40°) ≈10.9083

Die gesuchte Strecke ist nun gerade die Differenz der beiden Gegenkatheten:
s=35.717 - 10.908 ≈ 24.809 m.

Winkel zw. Punkten im Koordinatensystem

Beispiel:

Berechne alle Längen und Winkel im Dreick ABC mit A(-5|-3), B(4|4) und C(-5|4).

Runde die Ergebnisse auf eine Nachkommastelle.

Lösung einblenden

Wenn man die drei Punkte in ein Koordinatensystem einträgt, erkennt man sofort, dass (zwischen B und C) a = 9 und (zwischen A und C) b = 7 sein müssen. Weil das Dreieck rechtwinklig ist, kann man c (zwischen A und B), also die Hypotenuse, mit dem Satz des Pythagoras berechnen:

Dreiecks mit Hilfe des Satzes des Pythagoras berechnen.

c² = 9² + 7²

c² = 81 + 49

c² = 130

c = $\sqrt{130}$ ≈ 11.4

Da a (zwischen B und C) und b (zwischen A und C) parallel zu den Koordinatenachsen sind, muss der Winkel in C γ = 90° sein.

Den Winkel α können wir mit dem Tangens berechnen:

tan(α) = $\frac{Gegenkathete}{Ankathete}$ = $\frac{9}{7}$ ≈ 1.286

Daraus folgt: α = arctan(1.286) ≈ 52.1°.

Wegen der Winkelsumme von 180° im Dreieck folgt: β = 90°-52.1° = 37.9°

Strecken und Winkel im Dreieck

Beispiel:

Berechne alle Längen und Winkel im Dreick ABC mit A(-2|-1), B(1|2) und C(-2|4).

Runde die Ergebnisse auf eine Nachkommastelle.

Lösung einblenden

Wenn man die drei Punkte in ein Koordinatensystem einträgt, kann man nicht erkennen, dass das Dreieck rechtwinklig wäre, und man somit nicht direkt die Definitionen von Sinus uund Kosinus anwenden kann. Deswegen zeichen wir noch eine Höhe eine. Weil hier die Seite b parallel zur y-Achse verläuft, nehmen wir hier am besten die Höhe h_b.

Die achsenparallelen Strecken b und h_b kann man direkt ablesen:
b = 5 und h_b = 3

Weil Höhe ja parallel zur x-Achse verläuft, hat der Lotfußpunkt L, also der Punkt, wo die Höhe Höhe h_b auf b trefft, den gleichen y-Wert wie B, also y = 2.
Somit ergibt sich AL = 3 und LC = 2

Jetzt können wir mit dem Satz des Pythagoras in den beiden Teildreicken jeweils die Hypothenusen a und c berechnen:

c² = h² + AL² = 3² + 3² = 9 + 9 = 18

=> c = $\sqrt{18}$ ≈ 4.24

a² = h² + LC² = 3² + 2² = 9 + 4 = 13

=> a = $\sqrt{13}$ ≈ 3.61

Weil ja in beiden rechtwinkligen Teildreiecken () die Katheten achsenparallel und ganzzahlig sind, empfiehlt sich der Tangens zur Berechnung der Winkel:

Für den Winkel in A gilt: tan(α) = $\frac{Gegenkathete}{Ankathete}$ = $\frac{3}{3}$ = 1

Daraus folgt: α = arctan(1) ≈ 45°.

Für den Winkel in C gilt: tan(γ) = $\frac{Gegenkathete}{Ankathete}$ = $\frac{3}{2}$ = 1.5

Daraus folgt: γ = arctan(1.5) ≈ 56.3°.

Wegen der Winkelsumme von 180° im Dreieck folgt: β = 180°-45°-56.3° = 78.7°

Aufgabentypen anhand von Beispielen durchstöbern

Sinus und Thaleskreis (leicht)

Sinus und Thaleskreis (schwer)

Trigonometrie Anwendungen

Winkel zw. Punkten im Koordinatensystem

Strecken und Winkel im Dreieck